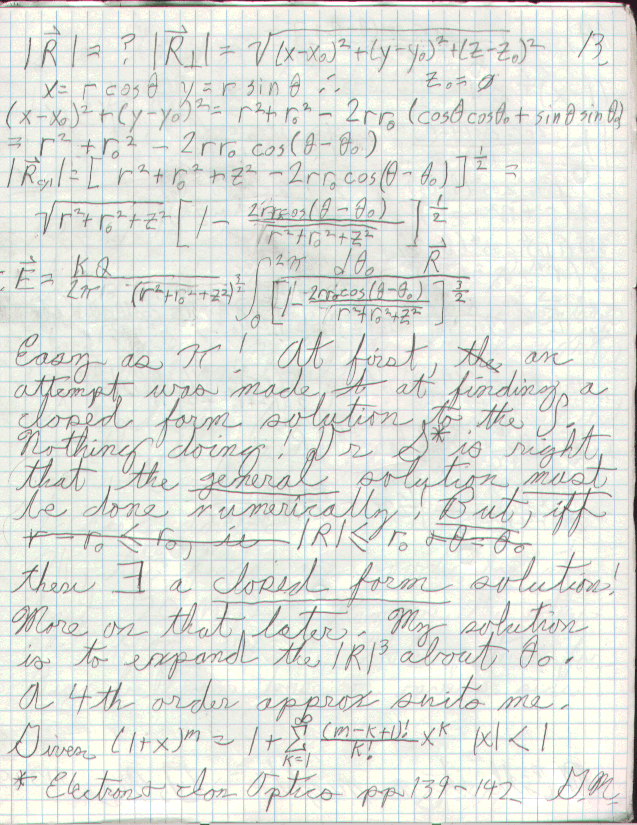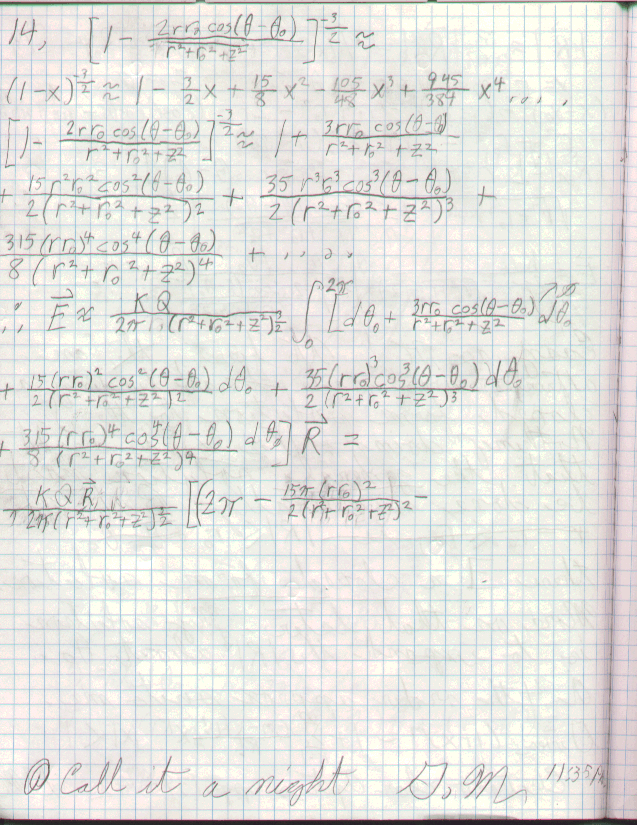Part II: Design Criteria:  Problems And Solutions

B.  Ion Optics, Sharp Edges, Points, Cracks and Other Sources of Grief (continued)

    iii.  The Electrodes  "Virtual Spherical Charged Shells"

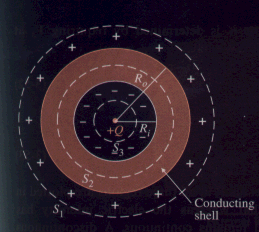
A canonical charged shell. [1]

Dr. Miley, at the U of Illinois, specifies that the electrodes should be within 3% of perfect sphericity and preferably more than 95% permeable to ion motion.  The latter really is only for the cathode.  Numerous "fusor" enthusiasts spot weld together their electrodes by hand.  This was done at the University Research Instrmentation Center on campus.  They did a nice job.  The anode was in fact, 97% permeable, but the cathode was only 75% free.  The constraint?  The T-304 stainless steel wire.  (The Farnsworth Hirsch team at ITT used T-304. [4]  There just happened to be a free source of it lying around.)  Still, as pretty as U.R.I.C.'s work was, the grid is only an approximation of a sphere.

A look at the electrodes before they were used extensively.

It is in fact, a fair approximation.  The grids consist of wire rings.  Under potential, these rings have a charge distibution on them.

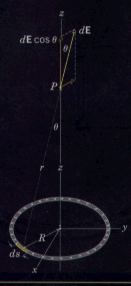
The textbook ring of charge problem.

This problem is no trifle when one leaves the axis of symmetry.

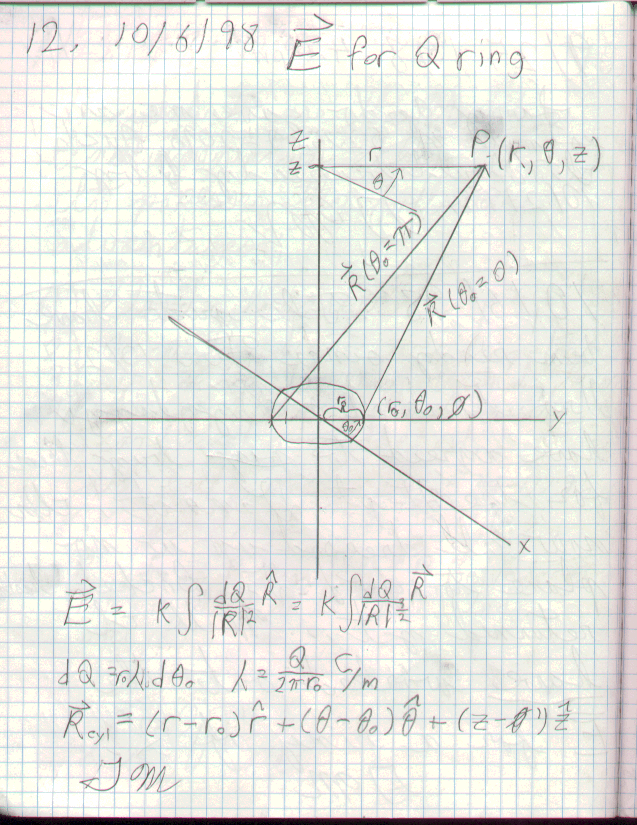
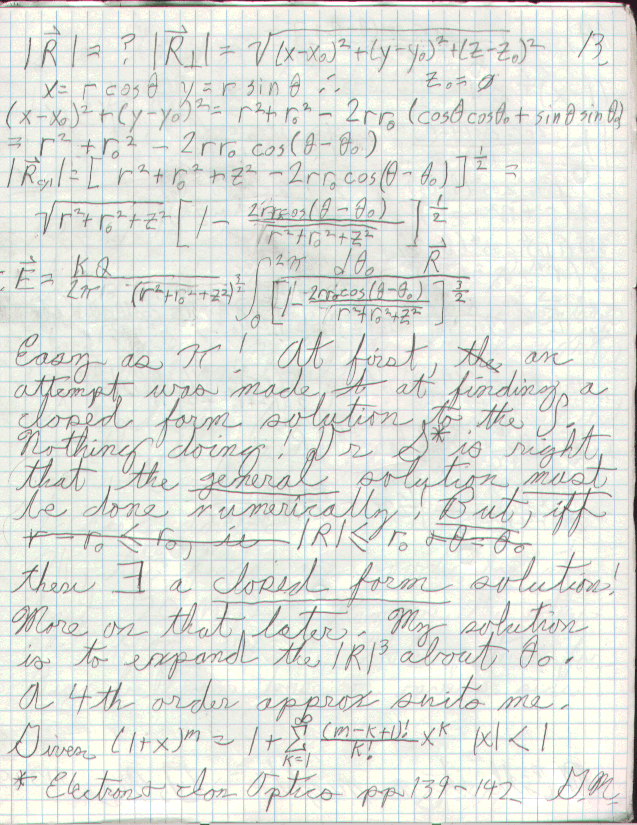
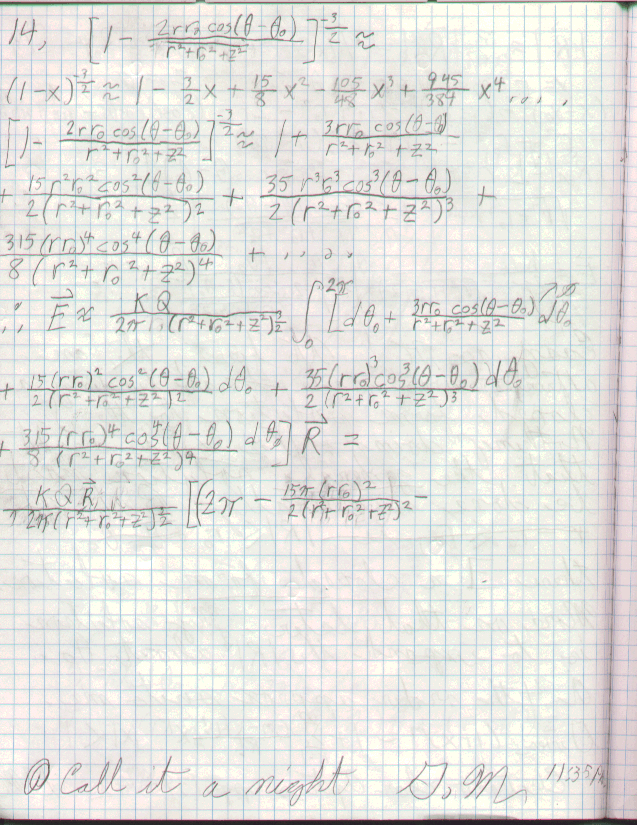
The Solution?

Rather than a numerical approximaxion, recall Gauss' Law:  D = Q/A.  Since the particular problem calls for only the region within the ring, the radius will never be greater in magnitude than R when calculating the normal area vector.  Therefore, the ring may be enclosed within a Gaussian torus of surface area 4pi^2R^2, rather than a sphere of area 4piR^2.  One then has but to superpose the contribution of each ring in the coordinate system.  Still ugly but it is a closed form solution!